Dr. Maryam Mirzakhani was an extraordinary mathematician whose influential work has had a profound impact on the field of mathematics, particularly in geometry and its applications. Born in Tehran, Iran, in 1977, Mirzakhani showed an early aptitude for mathematics, leading to a career marked by groundbreaking discoveries. In 2014, she became the first woman to be awarded the prestigious Fields Medal, often referred to as the “Nobel Prize of Mathematics,” which recognized her exceptional contributions toward understanding the symmetry of curved surfaces.
Contributions to Hyperbolic Geometry

One of Mirzakhani’s most notable contributions was in the realm of hyperbolic geometry. Hyperbolic surfaces, unlike the flat surfaces of Euclidean geometry, have constant negative curvature. Mirzakhani’s work primarily dealt with Riemann surfaces and moduli spaces of such surfaces. Her innovative methods allowed mathematicians to compute volumes of the moduli spaces of curves, providing new insights into the complex structure of these surfaces.
Her studies have applications that extend beyond abstract mathematics, influencing fields like complex systems, statistical mechanics, and even quantum field theory. The tools and methodologies she developed continue to assist researchers in exploring spaces that are curved and complex, impacting both mathematics and theoretical physics.
Ergodic Theory and Dynamics
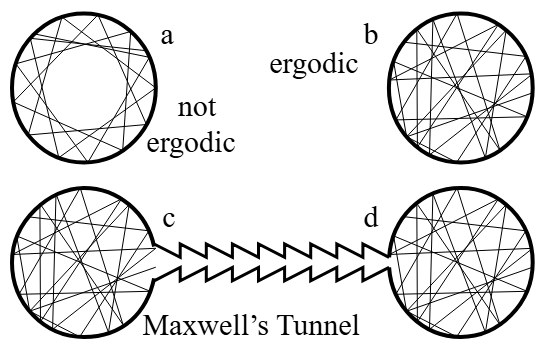
Mirzakhani made substantial strides in ergodic theory and the study of dynamical systems, particularly in understanding the behavior of billiard paths on polygonal surfaces. She explored the dynamics of billiard balls on such surfaces, which subsequently led to deeper insights into the behavior of geodesics on more complex surfaces. Her work in this area opened new avenues in understanding behaviors that are deterministic in nature but appear chaotic, therefore enriching the study of chaos in mathematics and physics.
Teichmüller Theory
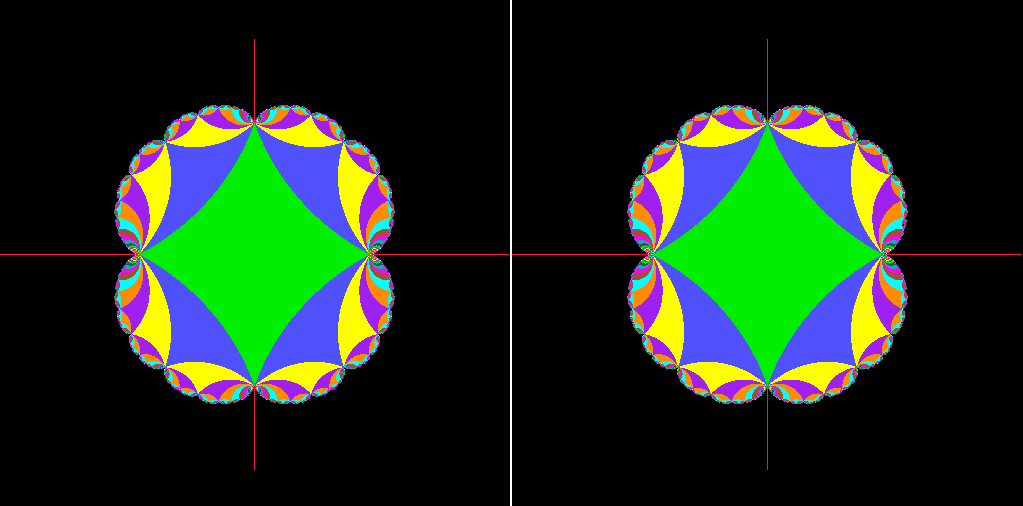
The Teichmüller space, a structure she probed deeply, is crucial in the geometric understanding of how complex structures deform. Mirzakhani’s work in this space involved connecting its geometric properties with theories of hyperbolic surfaces, leading to a greater understanding of surface topology and geometry. Her contributions helped solidify connections between algebraic geometry and low-dimensional topology, facilitating new research paths in mathematics.
Impact on Science and Beyond

The impact of Dr. Mirzakhani’s work extends beyond mathematics to influence scientific fields such as physics and engineering. Her intuitive approach to understanding geometry has helped develop mathematical tools crucial for scientists studying the properties of the universe, modeling natural phenomena, and even working with data structures in technology.
Beyond her technical contributions, Mirzakhani’s achievements have inspired many, particularly encouraging more young women to pursue mathematics and sciences. Her legacy continues not only through her mathematical insights but also in inspiring a new generation of mathematicians.
Conclusion

Dr. Maryam Mirzakhani’s work represents a remarkable fusion of abstract mathematics with practical applications that continue to influence various scientific fields. Her pioneering efforts in geometry and dynamics have enriched mathematical understanding and opened new horizons for exploration. As her legacy endures, Mirzakhani remains a beacon of inspiration, illustrating the profound impact one individual can have through curiosity, dedication, and a passion for discovery.




