Mathematicians all around have struggled with a theory so opaque for more than ten years that it was labeled the “alien’s language.” Developed by Japanese mathematician Shinichi Mochizuki, the Inter-universal Teichmüller Theory (IUT) runs over 2,000 pages and promises to solve the famous ABC conjecture a problem in number theory with great consequences for cryptography, quantum computing, even our understanding of prime numbers. Still, only a small number of academics could assert even partial understanding of Mochizuki’s writings until now. Then enter 28-year-old former doctoral student turned software engineer Zhou Zhongpeng, who has cracked IUT possibly opening its secrets for the larger mathematical world.
The “Alien” Theory That Baffled Mathematicians
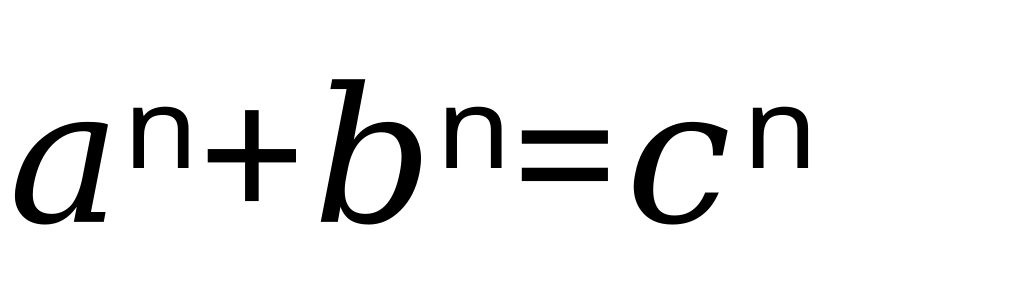
When Mochizuki first presented his IUT papers in 2012, the mathematical community was shocked not by clarity but by absolute inscrutability. Different from traditional mathematics, the theory presented whole new symbols, syntax, and conceptual frameworks that even leading experts battled to understand. Peer review has stayed frozen for years; only roughly 20 people worldwide have claimed any significant awareness of IUT.
The ABC conjecture, which IUT seeks to prove, is a deceptively simple statement about the relationship between prime numbers. If confirmed, it could revolutionize number theory, offering shortcuts to solving Fermat’s Last Theorem and other long-standing puzzles. Yet, Mochizuki’s proof was so arcane that some speculated it might be a deliberate intellectual fortress, a theory designed to be understood only by its creator.
Zhou Zhongpeng: The Outsider Who Cracked the Code
Zhou’s path into IUT defies convention as much as the theory itself. Having left academia to work as a software engineer, he was a former doctoral candidate in graph theory and stayed enthralled by pure maths. He spent five months carefully analyzing Mochizuki’s work in his free time. His breakthrough came when he discovered that, although requiring hundreds of pages of evidence, IUT’s ideas could be applied to generalised cases of Fermat’s Last Theorem, a problem famously solved by Andrew Wiles in 1995. Derived from IUT, Zhou’s method could produce the same outcome in far fewer steps.
His findings were so compelling that Ivan Fesenko, a mathematician who had previously worked on IUT, invited Zhou to Westlake University in China to collaborate. Now, under Fesenko’s mentorship, Zhou is refining his work potentially paving the way for broader acceptance of Mochizuki’s theory.
Why IUT Matters: From Cryptography to Quantum Computing

Should IUT prove valid, its ramifications go much beyond only mathematics.
- Cryptography: As it offers fresh understanding of the behavior of prime numbers, the foundation of RSA encryption 16, the ABC conjecture could destroy current encryption.
- Some physicists hypothesize that the abstract structures of IUT could reflect quantum error correction codes, necessary for the construction of stable quantum computers.
- Spacetime & Physics: Offering a fresh perspective on the fabric of the universe, IUT’s mathematical framework may even have resonance with ideas of quantum gravity.
However, the theory must first be converted into a language so the scientific community may grasp a job Zhou is now helping to progress. Only then will these opportunities come to pass.
The Controversy: Is IUT a Masterpiece or a Mirage?

Work by Mochizuki has been hotly debated. While some mathematicians, like Peter Scholze have freely questioned its validity, others, including Fesenko, argue that its complexity does not equal inaccuracy. The absence of peer-reviewed confirmation has left the theory in a state of flux, neither totally embraced nor discounted.
Zhou’s contributions could help to heal this split. By proving useful applications of IUT, he offers autonomous confirmation of Mochizuki’s theories. Still, a lot of the theory is untested, and, should it come at all, a full consensus may take years.
What’s Next? The Future of IUT and Mathematical Discovery

Zhou’s work is just the beginning. If his refinements hold, they could accelerate the adoption of IUT, leading to:
- New mathematical shortcuts for solving complex problems.
- Stronger interdisciplinary links between math, physics, and computer science.
- A potential paradigm shift in how mathematicians approach proofs, moving toward more abstract, interconnected frameworks.
Yet, as Zhou himself humbly notes, his contributions are “minor innovations” in a much larger puzzle. The full deciphering of IUT may still require a collective effort from the mathematical community.
Conclusion: A Step Closer to Understanding the “Alien” Math

The discovery by Zhou Zhongpeng reminds us that some of the most important scientific developments originate from unanticipated sources. A pure math enthusiast driven software engineer might have just opened the door to one of the most mysterious theories of our day. Whether IUT stands or falls, its narrative and Zhou’s part in it emphasizes the beauty and frustration of mathematical discovery: a language so deep that it can feel alien but so strong that it might change our perspective of reality itself.
Right now, the planet observes Zhou and Fesenko working one step closer to deciphering the “alien’s language”.
Sources:

Suhail Ahmed is a passionate digital professional and nature enthusiast with over 8 years of experience in content strategy, SEO, web development, and digital operations. Alongside his freelance journey, Suhail actively contributes to nature and wildlife platforms like Discover Wildlife, where he channels his curiosity for the planet into engaging, educational storytelling.
With a strong background in managing digital ecosystems — from ecommerce stores and WordPress websites to social media and automation — Suhail merges technical precision with creative insight. His content reflects a rare balance: SEO-friendly yet deeply human, data-informed yet emotionally resonant.
Driven by a love for discovery and storytelling, Suhail believes in using digital platforms to amplify causes that matter — especially those protecting Earth’s biodiversity and inspiring sustainable living. Whether he’s managing online projects or crafting wildlife content, his goal remains the same: to inform, inspire, and leave a positive digital footprint.




